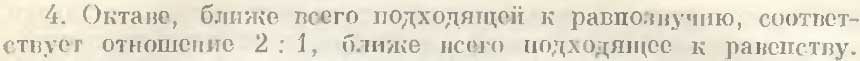|
7.3.2.1.4.2. Теория созвучных интервалов
|

|
Б. Л. ван дер Варден.
Пифагорейское учение о гармонии.
В книге: Б. Л. ван дер Варден.
Пробуждающаяся наука.
Математика древнего Египта, Вавилона и Греции.
М., Гос. изд-во физико-математической литературы, 1959, сс. 398 — 402.
Греческое понятие о созвучном интервале не совпадает с нашим понятием о консонансе. Два звука образуют созвучный интервал, если при одновременном их появлении они сливаются в единое впечатление.
Поэтому созвучными интервалами будут октава, квинта, составленная из октавы и квинты дуодецима, кварта, двойная октава, по Птолемею еще ундецима, по Аристоксену же, кроме того, и другие интервалы, большие двойной октавы, но только не большая и малая терции.
Последние, хотя и являются эммелическими, т. е. входят в хорошо звучащие гаммы и мелодии и красиво вместе звучат, но они не сливаются вместе и поэтому называются не симфонными, но диафонными. В этом согласны все наши источники.
Клавдий Птолемей, выдающийся астроном и теоретик музыки поздней древности, в первой книге своей "Теории гармонии" следующим образом излагает пифагорейскую теорию созвучных интервалов:
"Ухо признает следующие созвучные интервалы: так называемые кварту и квинту, разность между которыми называется целым тоном, затем октаву, ундециму, дуодециму и двойную октаву. Интервалы большие этих мы для нашей настоящей задачи должны оставить в стороне.
Пифагорейская теория из упомянутых интервалов оставляет в стороне также и ундециму в соответствии со своеобразными основными положениями, которые были главами этой школы выставлены из следующих соображений.
Особенно важным исходным пунктом в их методе является то, что равные числа сопоставляются с тонами одинакового напряжения, неравные же — с тонами разного напряжения.
Далее они говорят: подобно тому как существуют два основных различия тонов разного напряжения — симфонные и диафонные тона, из которых прекраснейшими являются симфонные, то и среди неравных чисел существуют два рода отношений, во-первых, так называемые сверхмерные, или как <меньшее> число к <большему> числу, а во-вторых, эпиморные, или же кратные (две величины находятся в кратном отношении (например, 2:1 или 3:1, если большая является кратной меньшей, а меньшая, таким образом, делителем большей; две величины находятся в эпиморном отношении (например, 3:2 или 4:3), если они имеют вид (n + 1):n для некоторого
натурального числа
n
— прим. редактора).
Более предпочтительными являются последние, вследствии простоты сравнения, так как для эпиморных отношений избыток является как раз некоторой дробной частью целого, в то время как в кратных отношениях меньшее число содержится в большем.
Поэтому они эпиморные и кратные отношения сравнивают с созвучными интервалами: октаву они выражают как отношение 2 : 1, квинту — как отношение 3 : 2, кварту — как отношение 4 : 3.
Это представляет несколько теоретический метод, поскольку он выражает следующее: из созвучных интервалов прекраснейшим является октава, а из числовых отношений лучшим — двухкратное. Октава — по той причине, что она ближе всего подходит к равенству напряжений, а двукратное потому, что только при этом отношении избыток является равным первоначальному числу.
Затем октава состоит из двух следующих один за другим первых созвучных интервалов — квинты и кварты, а двукратное отношение — из двух первых эпиморных, а именно 3 : 2 и 4 : 3.
Поскольку отношение 3 : 2 больше 4 : 3, то, следовательно, квинта будет больше кварты, так что их разность или целый тон стоит в отношении 9 : 8; именно настолько отношение 3 : 2 превосходит 4 : 3.
В соответствии с этим они причисляли к созвучным интервалам также дуодециму и двойную октаву, так как последняя соответствует отношению 4 : 1, а первая — 3 : 1. Ундециму же они не причисляли к созвучным интервалам, так как этот интервал соответствует отношению 8 : 3, которое не является ни эпиморным, ни кратным.
В соответствии с этим они добились тех же самых результатов при помощи следующего более геометрического способа. Представим себе некоторую квинту AB и, кроме того, еще новую квинту BC , так что AC будет двойной квинтой.
Поскольку двойная квинта не является созвучной, то AC не будет стоять в двойном отношении, поэтому и AB не будет в кратном отношении, но она является созвучным интервалом: следовательно, квинта соответствует эпиморному отношению.
Подобным же образом они доказывают, что кварта, которая меньше квинты, тоже соответствует эпиморному отношению.
Теперь, говорят они, представим себе октаву AB и затем еще одну октаву BC , так что AC будет некоторой двойной октавой.
Так как двойная октава будет созвучной, то AC будет соответствовать или эпиморному, или же кратному отношению. Но этот интервал не может соответствовать эпиморному отношению, ибо тогда его нельзя было бы разделить пополам; следовательно, AC, а значит и AB, будут соответствовать кратному отношению; таким образом, октава будет иметь кратное отношение.
Отсюда они выводят очевидное заключение, что октава соответствует отношению 2:1, квинта — отношению 3:2 и кварта — отношению 4:3."
Мы имеем все основания полагать, что относительно пифагорейской теории музыки Птолемей имел сведения из лучших научных источников. Хотя он критикует данное пифагорейское обоснование, его изложение является логическим и лишенным противоречий, совершенно противоположно спорным филолаевским фрагментам.
Он также не рассказывает никаких мифов о
Пифагоре, как это охотно делают его современники, но в качестве наиболее выдающегося теоретика музыки он называет старшего современника
Платона, а именно Архита Тарентского, относительно
системы интервалов которого он кажется хорошо осведомленным.
Вторым признаком подлинности является то, что система интервалов Архита отличается от принятой в
Платоновском "Тимее".
Наконец, следует еще упомянуть, что его изложение второго "более геометрического" способа обоснования точно совпадает с почти на пятьсот лет более старшим "Sectio canonis".
В вышеприведенном изложении Птолемея упоминаются два способа обоснования. Первый, более первоначальный, исходит из следующих четырех постулатов:
Кроме того, доказательство основывается на следующих трех положениях теории чисел:
(i)
Кратное отношение, будучи удвоено (т. е. по современному способу выражения, возведено в квадрат), дает снова кратное отношение.
(ii)
Если числовое отношение после удвоения дает кратное отношение, то оно само будет кратным.
(iii)
Между двумя числами, стоящими в эпиморном отношении, нельзя найти ни одной, ни нескольких средних пропорциональных.
Из этих предложений первое является самоочевидным, а второе равносильно предложению 7 VIII книги "Начал" Евклида.
Предложение (iii) приписывается Боэцием Архиту. Приводимое Боэцием доказательство Архита, согласно Таннери, во всех существенных пунктах совпадает с доказательством в "Sectio".
Оно основывается на предложении 8 VIII книги "Начал" Евклида: если между двумя числами можно вставить другие числа в непрерывной пропорции, то такое же количество чисел в непрерывной пропорции можно вставить между двумя любыми числами, имеющими то же самое отношение, и, значит, в частности, между наименьшими числами, имеющими равное отношение.
Совпадение хода мыслей в доказательстве, приведенном Боэцием, с ходом мыслей в доказательстве "Sectio canonis" показывает, что Боэций заимствовал его из хорошего специального научного источника.
Поэтому мы можем поверить и его свидетельству, что данное предложение и доказательство восходят к Архиту. Но отсюда получаются два важных следствия.
Во-первых, Архит предполагает уже известной теорему 7 VIII книги "Начал" Евклида, хотя она ничуть не является самоочевидной. Отсюда следует, что тогда уже существовала теория чисел, обнимавшая большую часть VII и VIII книг "Начал" Евклида.