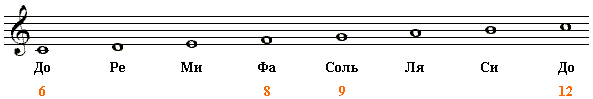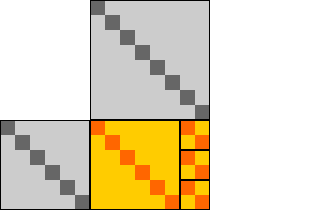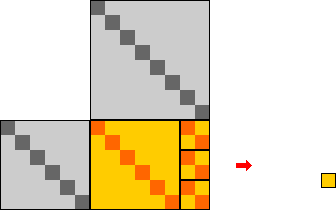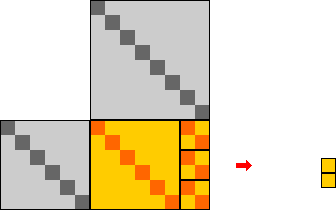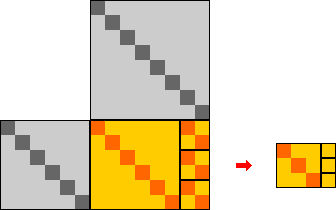|
7.3.2.2. Музыкальная шкатулка
|

|
В данном Разделе нас будет интересовать
возможность визуализации математических принципов,
положенных
Пифагором и пифагорейцами в основу устройства
музыкальной шкалы.
Впоследствии эти принципы, конечно, мутировали, но в своей глубинной сущности сохранились до сих пор.
Можно даже выделить
базовую структуру "музыкальной гармонии", которая лежала в основе всего:
она была связана с четырьмя числами:
6, 8, 9, 12. Две разные легенды об их открытии Пифагором
приведены
здесь и
здесь
(в
фундаментальном труде Б. Л. ван дер Вардена, посвященном анализу пифагорейского учения о гармонии,
упоминания об этих числах встречаются чуть ли не на каждой странице).
Ниже изображено примерное соответствие этих чисел со звуками "современной музыкальной шкалы".
Когда говорили, что между "звуками"
8 и
6,
а также между "звуками"
12 и
9
лежит интервал
величиной в кварту, то подразумевали под этим, что упорядоченная пара чисел
<4, 3> является
наименьшей парой
как для пары
<8, 6> так и для пары
<12, 9>
(я здесь использую обычное теоретико-множественное обозначение для упорядоченных пар:
посредством
<m, n> обозначается упорядоченная пара с первым элементом
m и вторым элементом
n).
То есть значительную роль здесь играла задача приведения данной упорядоченной пары
натуральных чисел к
наименьшей паре;
таким образом происходило вычисление
"стандартных" значений для
содержащихся в тетраде консонансов:
<2, 1> для октавы,
<3, 2> для квинты и
<4, 3> для кварты.
В традиционной школьной арифметике этому отвечает задача
сокращения соответствующих дробей.

|
Так, например, звук, соответствующий числу 6,
визуализируется посредством серого квадрата размером 6 у. е.,
а звук, соответствующий числу 8 —
посредством серого квадрата размером 8 у. е.
Если мы совместим эти квадраты друг с другом "уголками",
как показано на рисунке слева, то получим в результате конструкцию,
которая ранее была названа
"рамкой".
Затем, стандартным способом вставив
в эту "рамку" соответствующий евклидов прямоугольник,
мы получим визуальный образ музыкального интервала, заключенного между звуками,
изображенными при помощи серых квадратов.
Отметим, что по соглашению со
Страницы 7.1.2.3, полученному в данном случае евклидову прямоугольнику
будет соответствовать упорядоченная пара <8, 6>
(как это и должно быть для интервала, лежащего между
"звуками" 8 и 6).
|
Визуальным же аналогом задачи приведения данной упорядоченной пары натуральных чисел к
наименьшей паре будет
задача приведения соответствующего евклидова прямоугольника к
редуцированному виду.
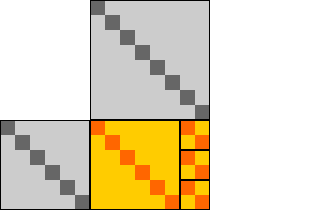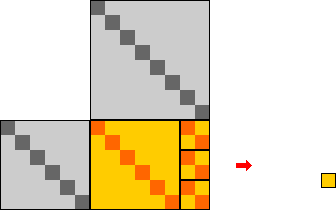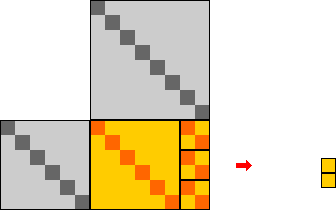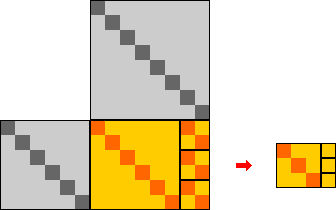
|
В данном случае в результате решения этой задачи мы получаем стандартное "визуальное представление"
для консонанса кварты (которое уже было изображено
ранее).
По соглашению со Страницы 7.1.2.3, полученному окончательно евклидову прямоугольнику
будет соответствовать упорядоченная пара <4, 3>
(как и положено для "стандартного" значения консонанса кварты).
|
Зачем нужна вся эта визуализация? Ведь сокращение дробей, подобных
8/6 или
12/9, взрослые люди обычно производят
автоматически, не испытывая при этом ни малейших затруднений.
Впрочем, конечно, это еще как посмотреть... Существуют же
Павлы, мыслящие более визуально, чем Петры.
Кроме того, можно вдохновиться
мыслями Мэрили Зденек
и рассматривать представленную ниже "музыкальную шкатулку" как один из многочисленных тренингов
по развитию способностей
правого полушария головного мозга.
Но дело даже не в этом. Что толку с того, что люди обычно могут быстро производить в уме сокращения небольших дробей?
Ведь они делают это бездумно, автоматически применяя правила,
вложенные в их мозг на протяжении обучения в школе.
Они не видят стоящих за этим
идей и, следовательно, не чувствуют
"глубоко" соответствующие
математические конструкции. Короче говоря, они ведут себя как
описанный Полем Сурье "алгебраист":
Знает ли алгебраист, что происходит с его идеями, когда с помощью
знаков он их вводит в свои формулы? Прослеживает ли он за ними на
протяжении всех этапов, которые он осуществляет? Без сомнения, нет.
Он их тотчас же теряет из поля зрения. Он заботится лишь о том,
чтобы упорядочивать и комбинировать, в соответствии с известными
правилами, материальные знаки, находящиеся у него перед глазами;
и он принимает полученный результат как вполне надежный.
Создание
"чисто визуального арифметического языка", при манипулировании с
которым "идеи" не терялись бы из виду, было одной из основных целей построения
"арифметики на квадратах". Конечно, этот язык очень необычен, однако при систематическом
изучении он позволяет сформировать новое видение "арифметической реальности",
при котором глубинный смысл математических конструкций начинает просматриваться яснее.
Мы переходим теперь к описанию
"музыкальной шкатулки", призванной "чисто визуально" показывать
содержащиеся в тетраде гармонические интервалы.
Как всегда, имеются две версии программы:
Версия B раскрывается на весь экран,
тогда как
Версия А работает в стандартном окне броузера
(чтобы вернуться из "Версии В" обратно, нажмите на клавиатуре CTRL + W).
Шкатулка функционирует в соответствии с принципами, изложенными
выше. Т. е. звуки, отвечающие числам
6, 8, 9, 12 представлены в виде серых квадратов, которые могут
"ездить" по экрану и соединяться друг с другом "уголками", образуя "рамки". Затем в эти рамки
вставляются евклидовы прямоугольники, символизирующие музыкальные интервалы и, наконец,
осуществляется процедура редукции евклидового прямоугольника с целью получения "стандартного"
значения для соответствующего консонанса.
Как известно, тетрада содержит в себе
октавный интервал, затем —
два интервала величиной в
квинту (вехняя и нижняя квинты), далее —
два интервала величиной в
кварту (вехняя и нижняя кварты) и, наконец, —
интервал между квартами (т. е. между "звуками"
9 и
8).
Последний интервал не является консонансом, он представляет собой
целый тон
(в
античном понимании этого слова).
Чтобы увидеть все эти интервалы, откройте программу и наведите указатель мыши на надпись
"Показать". Затем выберите в появившемся меню тот интервал, который вы желаете увидеть, и наблюдайте ассоциированную
с ним анимацию. После завершения анимации вы можете запустить ее снова для какого-нибудь
другого интервала, выбранного из меню.
Имеется возможность регулировки скорости протекания отдельных этапов анимации.
В поле под кнопкой "Скорость1" находится значение скорости движения серых квадратов до того момента,
пока они не соприкоснутся "уголками". В поле под кнопкой "Скорость2" находится значение скорости
осуществления процесса редукции евклидова прямоугольника. Оба значения скорости даны в миллисекундах.
Вы можете изменить значения этих скоростей, установленные по умолчанию. Для этого введите в соответствующее поле
свое значение и после этого обязательно нажмите кнопку, расположенную над полем,
чтобы вновь введенное значение установилось.