ABSTRACT: Although mathematical models of the scale have always been characteristic of Western music theory, in the last 200 years they have not been very much improved (although some interesting properties of scales have been defined in recent years).

РЕЗЮМЕ: Хотя математические модели (музыкальных) шкал всегда были характерны для западной музыкальной теории, за последние 200 лет эти модели не претерпели существенного улучшения (несмотря на то, что в последние годы были установлены некоторые интересные свойства этих шкал).

This article describes our effort in a new book to contribute to this part of music theory by using some appropriate concepts of modern algebra.

В данной статье изложены наши усилия по написанию одной новой книги, призванной внести определенный вклад в эту часть музыкальной теории посредством использования некоторых понятий современной алгебры.

[1] Our sequence of mathematical constructions is listed in Fig 1.

[1] Our sequence of mathematical constructions is listed in Fig 1.

Fig 1. A sequence of constructions abstracted from the pitch continuum:

Fig 1. A sequence of constructions abstracted from the pitch continuum:

a) a positive-number line for pitch frequencies;

b) a number line for logarithms to base 2 of the frequencies;

с) equivalence classes of points mod 1 on this number-line (flogs);

d) pitch-class relations between these equivalence classes (also flogs);

e) two kinds of generators for groups of pitch-class relations: equal-division (1/n converted to a flog) or harmonic (see below);

f) the pairs, (set, Abelian group), which ensue from these generators;

g) equivalence-class neighborhoods around every point-mod-1 in this set;

h) "ideal systems", whereby every system comprises a pair: a finite set of non-overlapping neighborhoods, operated upon by a subset of one of our groups (that is, by a "halfgroup");

i) unlimited scales (repeating in every octave indefinitely);

j) scales with a highest and lowest note.

a) a positive-number line for pitch frequencies;

b) a number line for logarithms to base 2 of the frequencies;

с) equivalence classes of points mod 1 on this number-line (flogs);

d) pitch-class relations between these equivalence classes (also flogs);

e) two kinds of generators for groups of pitch-class relations: equal-division (1/n converted to a flog) or harmonic (see below);

f) the pairs, (set, Abelian group), which ensue from these generators;

g) equivalence-class neighborhoods around every point-mod-1 in this set;

h) "ideal systems", whereby every system comprises a pair: a finite set of non-overlapping neighborhoods, operated upon by a subset of one of our groups (that is, by a "halfgroup");

i) unlimited scales (repeating in every octave indefinitely);

j) scales with a highest and lowest note.

Our point of departure is the pitch continuum, which is not a mathematical construction but an intuition, since pitch is subjective. (Pitches as we hear them cannot be measured, but only judged.)

Нашей отправной точкой является континуум питчей, который сам по себе не является какой-либо математической конструкцией, а является, скорее, некоторым интуитивным понятием, поскольку питч субъективен. (Питчи, в том виде как мы слышим их, не могут быть измерены, а могут только оцениваться.)

Our first construction is a positive-number line for the sound-wave frequencies, which can be measured and which almost wholly determine the pitches.

Нашей первой математической конструкцией является числовая прямая с положительными числовыми отметками для частот звуковых волн, которые могут быть измерены и которые почти полностью определяют питчи.

[2] It is the differences between pitches that interest us musically.

[2] Имеются определенные различия между питчами, которые интересуют нас с музыкальной точки зрения.

Experience teaches us that there is a logarithmic relation between these subjectively judged differences and the differences among the corresponding pitch frequencies.

Опыт учит нас, что существует некоторая логарифмическая связь между этими субъективно оцениваемыми различиями и различиями между соответствующими частотами питчей.

So our second construction is a number line for the logarithms of the frequencies.

Таким образом, нашей второй конструкцией является числовая прямая для изображения логарифмов этих частот.

We use logarithms to the base 2; this choice is due to another aspect of musical experience: the musical interval between two notes whose frequencies are in the ratio 2:1 is an octave, and notes one or more octaves apart from each other are intuitively heard as manifestations of the same note on different levels.

Мы используем логарифмы по основанию 2; этот выбор обусловлен еще одним аспектом музыкального опыта: музыкальный интервал между двумя нотами, частоты которых находятся в отношении 2:1, является некоторой октавой, и ноты, отстоящие друг от друга на одну или более октав, интуитивно воспринимаются слухом как проявления одной и той же ноты на разных уровнях.

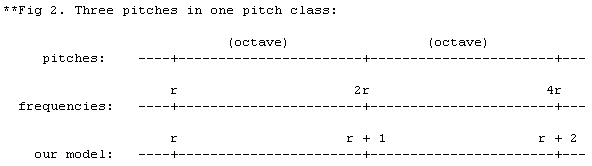
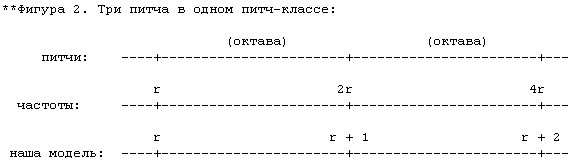
Normally a scale repeats itself in each octave (there are exceptions, but they can be treated as special cases), so musicians today speak of pitch classes (see Fig 2) — that is, of equivalence classes of notes that are one or more octaves apart from each other — and of "pitch-class intervals" or "pitch-class relations", which are the analogous equivalence classes of musical intervals.

Обычно шкала повторяет саму себя в каждой октаве (существуют исключения, но они могут рассматриваться как особые случаи). Вследствие этого музыканты сегодня говорят о "питч-классах" (см. Фигуру 2) — то есть о классах эквивалентности нот, отстоящих друг от друга на одну или более октав — и о питч-классах интервалов (или "питч-классах отношений"), которые являются аналогами классов эквивалентности музыкальных интервалов.

With logarithms to the base 2 it is very easy to define the addition of logarithms-mod-1 (which we call "flogs") in such a way that the sum will be musically valid when the flogs for two pitch-class relations are added.

Используя логарифмы по основанию 2, можно легко определить сложение "логарифмов по модулю 1" (которые мы называем "flogs" или "флогсами") таким образом, чтобы эта сумма была бы приемлемой с музыкальной точки зрения в контексте процесса, при котором складываются друг с другом "флогсы" двух питч-классов отношений.

[3] For a simple example, let us see how the flog for a 5th with a frequency ratio of 3:2, when added to itself, yields a flog for a whole-tone.

[3] В качестве простого примера, давайте посмотрим, как flog для квинты с отношением частот 3:2, будучи сложенным сам с собой, дает flog для целого тона.

It is readily reckoned that, to three decimal places, log 3 to the base 2 = 1.585, and hence log (3/2) to the base 2 = 0.585.

Нетрудно вычислить, что с точностью до трех десятичных знаков после запятой, логарифм трех по основанию два равен 1.585, и, следовательно, log (3/2) по основанию два равен 0.585.

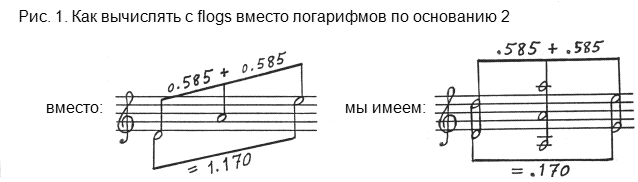
Now instead of adding 0.585 + 0.585 and getting 1.170 for a major 9th (which differs by 1 from the log for a whole-tone), we reckon in terms of flogs and write .585 + .585 = .170. This is illustrated in GIF 1.

Теперь вместо того, чтобы складывать 0.585 + 0.585 и получать в результате 1.170 для большой ноны (которая отличается на 1 от логарифма по основанию 2 для целого тона), мы проводим вычисления в терминах flogs и пишем: 0,585 + 0,585 = 0,170. Это проиллюстрировано на Рис. 1.

[4] According to Max Weber³, there are two rational ways to construct a system of tones: by means of harmonic relations or else by dividing the octave into equal parts.

[4] Согласно Максу Веберу³, существует два рациональных способа построить некоторую систему тонов: либо при помощи гармонических отношений, либо посредством деления октавы на равные части.

³Max Weber, *Die rationalen und soziologischen Grundlagen der Musik*, ed. Theodor Kroyer (Munich 1921). (The English translation published in 1958 is, alas, so inadequate that it quite misrepresents Weber's thinking.)

³Max Weber, *Die rationalen und soziologischen Grundlagen der Musik*, ed. Theodor Kroyer (Munich 1921). (Английский перевод этой книги, опубликованный в 1958 году, является, к сожалению, настолько неадекватным, что совершенно искажает образ мышления Вебера.)