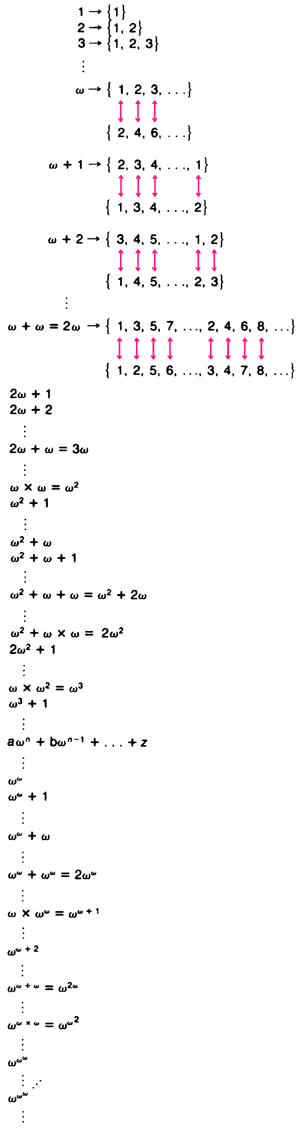|
9.3.1.4. Трансфинитные
ординальные числа
©
|

|
Аналогичным образом он первоначально называл символы
∞, ∞ + 1, ∞ + 2, ... только средством для обозначения множеств. Но в 1883 г. он объявил их
трансфинитными числами, самостоятельным и систематическим обобщением
натуральных чисел.
Как указывал Кантор, непосредственным поводом для введения этих чисел было то, что они оказались необходимыми для дальнейшего развития теории множеств и изучения действительных чисел. Тем не менее, чтобы ответить критикам
вроде Кронекера, Кантор отстаивал правомерность этих чисел в математике и со своей
философской позиции: как только
непротиворечивость трансфинитных чисел признана, их уже нельзя отвергать, как и другие принятые, но сразу же поставленные под сомнение числа вроде иррациональных.
Формулируя теорию бесконечности, дающую возможность избежать известные математические парадоксы, Кантор верил, что он устранит единственно обоснованное возражение, которое могли выдвинуть математики против узаконивания понятия завершённой бесконечности.
Поэтому значительный исторический интерес представляет то, что первыми трансфинитными числами были не кардинальные числа, а ординальные.
Ординальное число определяется его порядком или положением в некотором перечне. Ординальное число, ассоциируемое с конечным множеством, соответствует кардинальному числу этого множества.
Например, всякое множество, состоящее из пяти элементов (т.е. всякое множество, кардинальное число которого равно пяти), можно в некотором роде мыслить как непосредственно следующее за любым множеством из четырёх элементов. Другими словами, ординальное число этого множества тоже равно пяти; оно является пятым множеством в перечне множеств.
Однако ординальное число бесконечного множества следует отличать от его кардинального числа.
Кантор показал, что можно построить бесконечное число бесконечных множеств, имеющих различные ординальные числа, но одно и то же кардинальное число. Фактически Кантор позднее сумел превратить это свойство бесконечных множеств в критерий отличия их от конечных множеств: множество конечно, если его кардинальное и ординальное числа совпадают.
Кантор показал, что ординальное число последовательности конечных множеств возрастающей величины 1, 2, 3, ... получается путём повторного прибавления единицы.
Не существует наибольшего ординального числа, ассоциированного с последовательностью конечных множеств, но, так же как возможно определить иррациональное число π в виде предела последовательности рациональных чисел, можно, как считал Кантор, определить новое, трансфинитное ординальное число ω как первое число, следующее за всей последовательностью чисел 1, 2, 3, ... .
Как только ω определено, становится возможным путём последовательного прибавления единицы порождать другие трансфинитные ординальные числа:
ω + 1, ω + 2, ω + 3, ... .
Поскольку у этой последовательности не существует наибольшего элемента, то можно представить следующее ординальное число ω + ω или 2ω в виде первого ординального числа, следующего за последовательностью ω + 1, ω + 2, ω + 3, ... . Повторяя поперемено эти два принципа порождения, Кантор определил некую иерархию трансфинитных ординальных чисел [см. рисунок ниже].
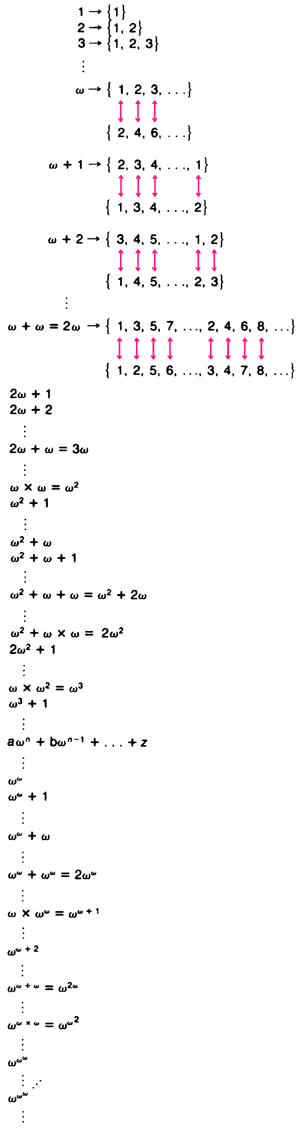
|
Трансфинитные ординальные числа определяются их порядком или положением в некотором перечне. Этот перечень порождается в соответствии с двумя принципами.
Во-первых, каждое новое ординальное число получается из непосредственно предшествующего ординального числа добавлением одной единицы, в точности также как если бы мы «считали» за пределами трансфинитного ординального числа ω, т.е. числа, связанного с множеством целых чисел, расположенных в их естественном порядке.
Во-вторых, если существует последовательность трансфинитных ординальных чисел, у которой нет наибольшего числа, то новое ординальное число определяется как следующее число, большее всех остальных чисел последовательности. Такие числа помещаются в перечне непосредственно после отметки пропуска.
Например, 2ω представляет собой следующее трансфинитное ординальное число, большее всех чисел ∞, ∞ + 1, ∞ + 2, ... .
На рисунке представлены два примера множеств, соответствующих ординальным числам ∞, ∞ + 1, ∞ + 2, и 2ω.
Однако всякое бесконечное множество, представляемое ординальным числом этого перечня, имеет одно и то же кардинальное число, а именно —
א0א, другими словами, каждое множество содержит одно и то же число элементов.
Каким образом можно провести различие, скажем, между ординальными числами ω и ∞ + 1? Различие определяется порядком элементов в множествах, которым соответствуют ω и ∞ + 1.
Например, множество натуральных чисел в их известной последовательности (1, 2, 3, ...) имеет ординальное число ω, представляющее всю последовательность натуральных чисел в её обычном порядке.
Однако множество всех натуральных чисел в перестроенной последовательности (2, 3, 4, ..., 1) или же множество всех натуральных чисел в последовательности (10, 30, 40, ..., 20) имеет ординальное число ∞ + 1.
Другими словами, это различие зависит от порядка следования элементов в последовательности и от размещения бесконечно длинных пробелов, помеченных многоточием. Если в конце последовательности находится одно число, то ординальным числом новой последовательности будет ∞ + 1.
Последовательность (2, 4, 6, ..., 1, 3, 5, ...) имеет два бесконечных пробела, и её ординальное число равно ω + ω или 2ω.
Отметим, что все эти множества имеют одно и то же число элементов, т.е. между самими этими множествами, а также между каждым из этих множеств и множеством целых положительных чисел можно установить взаимно однозначное соответствие.
Поэтому их кардинальные числа одинаковы, хотя их ординальные числа различны.
|
Определив трансфинитные ординальные числа, Кантор приступил к описанию их арифметических свойств. Между трансфинитными и обычными числами следует провести важное различие в отношении свойства коммутативности для сложения и умножения.
Для двух обычных чисел A и B свойство коммутативности выражает тот факт, что (A + B) равно (B + A) и (A × B) равно (B × A).
Однако, что касается трансфинитных чисел, свойство коммутативности уже не может быть гарантировано. Например, ∞ + 2, представляющее последовательность
(1, 2, 3, ..., 1, 2), не равно 2 + ∞ , представляющему последовательность (1, 2, 1, 2, 3, ...).
Поскольку понятия ординального и кардинального числа для
бесконечных множеств существенно различны, то при рассмотрении числа, ассоциированного с бесконечным множеством, всякое рассуждение, не учитывающее это различие, может привести к неясности. Таким образом, на бесконечные множества нельзя распространять кажущиеся очевидными свойства конечных множеств, как это делали
Галилей и другие.