Начало см. здесь.

1. Свободные моноиды с двумя образующими

Выше было указано, что особую роль в наших рассмотрениях будут играть свободные полугруппы и моноиды (с двумя образующими). Анонсированный там способ разметки вершин Дерева Штерна-Броко цепочками в алфавите {V, H} (показанный пока только для вершин 2-го уровня этого Дерева) открывает путь к естественной "автоматной" интерпретации всех наших конструкций.

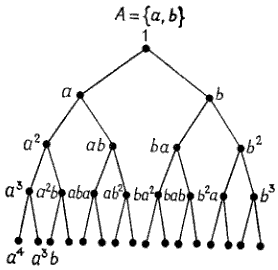
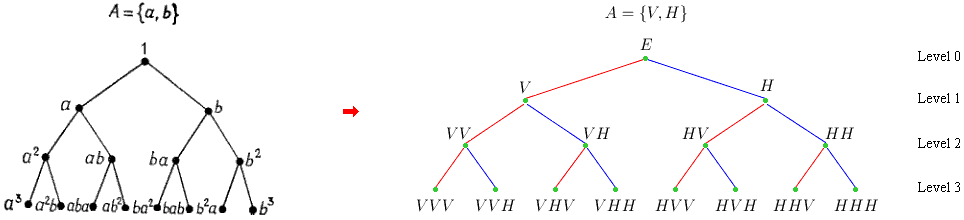
Подружить размеченное таким образом Дерево Штерна-Броко с автоматами проще всего при помощи классического материала, изложенного у Ж. Лаллемана здесь и здесь. Его нужно адаптировать к нашему случаю и это можно сделать очень просто. Для начала исходим из дерева у Лаллемана, вершины которого помечены цепочками в бинарном алфавите A = {a, b}:

и переходим от него к нужному нам Дереву, вершины которого помечены цепочками в бинарном алфавите A = {V, H} (символ E в нашем случае обозначает пустую цепочку):