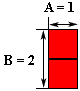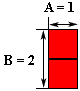Начало см. здесь.

"Данная визуализация" была приведена выше.

Задача на построение, которую предлагается рассмотреть в контексте этой визуализации, сформулирована во 2-ом предложении VIII книги "Начал" Евклида: "Найти наименьшие числа в непрерывной пропорции, сколько бы их ни было назначено, в заданном отношении" (Комментарий Д. Д. Мордухай - Болтовского к этому Предложению см. здесь). Как и у Евклида, мы будем считать, что назначено четыре числа, которые мы будем обозначать I, H, G, K, и что заданное отношение в наименьших числах есть A:B = 1:2.

Исходное отношение в наименьших числах A:B = 1:2 может быть визуализировано следующим образом:

То есть, оно может быть визуализировано в виде заложенного квадратной красной плиткой прямоугольника, длина горизонтальной стороны которого равна 1 у. е., а длина вертикальной стороны равна 2 у. е. Отношение, ассоциированное с такого рода прямоугольниками, моделируется отношением длины их горизонтальной стороны к длине их вертикальной стороны.

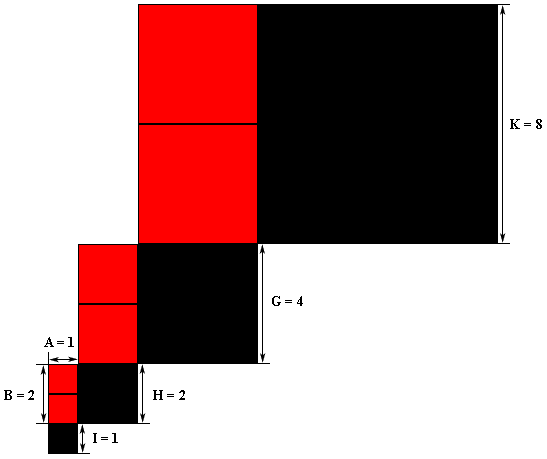
Забегая вперед и считая задачу уже решенной, мы можем изобразить в рамках предложенной визуализации связь заданных величин A = 1, B = 2, и полученных в результате решения задачи значений искомых величин I, H, G, K, следующим образом:

Значения четырех искомых величин I, H, G, K моделируются на представленной композиции длинами сторон четырех черных квадратов, фигурирующих на композиции. Важно отметить, что значения этих величин могут быть получены не путем измерения, а только лишь из исходных величин A, B путем размышления в терминах законов Кирхгофа (по методологии, которая для общего случая подробно разбирается у И. М. Яглома здесь и здесь.