Начало см. здесь и здесь.

Полюбившейся мне паттерн можно легко и с большой образовательной пользой получать на основе рассмотрения какого-либо рационального луча, проведенного на плоской квадратной целочисленной решетке точек. Рассмотрим, например, следующий рациональный луч и выделим на координатной плоскости прямоугольник, охватывающий первые четыре целочисленные точки, лежащие на этом луче:

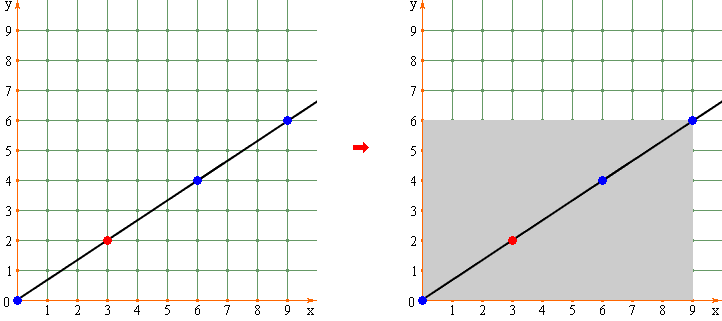
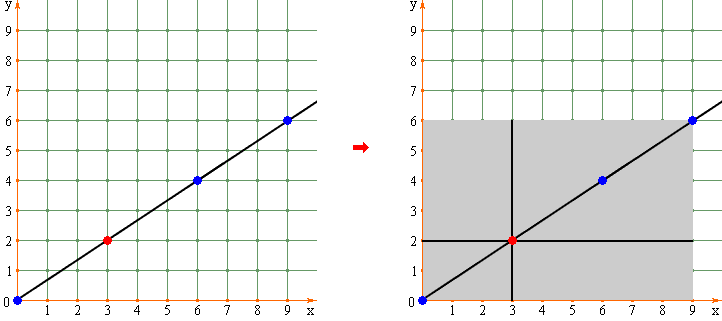
Очевидно, этот прямоугольник будет координатным прямоугольником 3-ей точки данного рационального луча (согласно определению "координатного прямоугольника некоторой точки", приведенного, например, у Делоне-Райкова здесь и здесь, а также согласно принятой нумерации целочисленных точек рациональных лучей). На каждом рациональном луче существует единственная видимая точка. Проводим через нее два отрезка и разбиваем серый прямоугольник на четыре прямоугольные области:

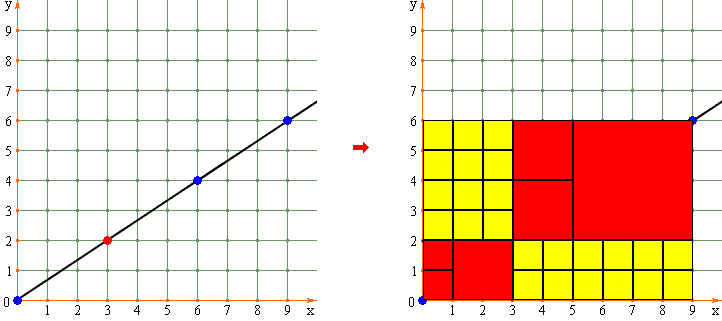
Теперь по накатанной методологии закладываем эти области разноцветной квадратной плиткой и получаем рассмотренный выше "дискретный" паттерн, на котором можно эффектно показать уйму ценнейших математических конструкций.