Подбираемся к комбинатору B со стороны импликативных пропозициональных исчислений

Лично я "въезжал" в мат. логику по учебнику С. К. Клини. Но потом убедился, что "чемпионом" в плане доходчивости и понятности при первоначальном изучении мат. логики будет, наверное, "Формальная логика" под ред. Чупахина И.Я., Бродского И.Н. Несмотря на обильное использование в ней (местами) марксистско - ленинской фразеологии. В особенности это касается очень доходчивого изложения проходящей красной нитью через весь их курс (и очень важной для нас в этом Разделе) методологии анализа кратных импликаций.

Мы будем (формально) интерпретировать типы как кратные импликации и начнем постижение сути комбинатора B в рамках типовой комбинаторной логики.

Обычно импликативные пропозициональные исчисления формулируются таким образом, что важным правилом вывода в них является правило Modus Ponens (Модус Поненс) (см. также в алгебраической интерпретации у Е. Расевой здесь; соотношение (1) на странице по указанной ссылке).

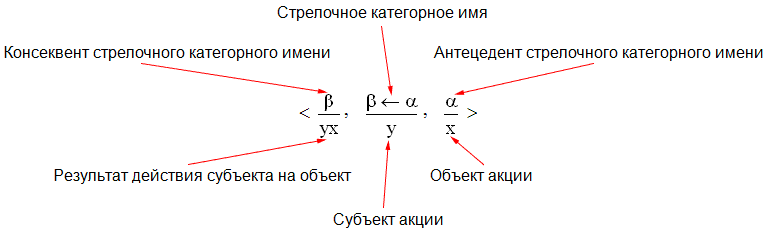
Формально правило Modus Ponens используется при формировании типовых термов в типовой комбинаторной логике (пункт (b) в Определении 4. 1). Также это правило существенным образом используется при определении Акции, чтобы отобразить то обстоятельство, что субъект акции активен по отношению к ее объекту, может действовать на него и дать какой-то результат этого действия.

Базовые интуиции для такого подхода к экспликации понятия "акция" приведены здесь. Уточнение этих интуиций для Исчисления Локализованных Цепочек (LCC), ассоциированного с некоторой Грейбах-грамматикой, изложено здесь (в этом случае результатом действия субъекта y на объект x является конкатенация yx цепочек y и x).

Отмеченные выше подходы являются на самом деле органичной частью большого потока исследований по так называемым "формулам типам". Ниже приведен краткий обзор этих исследований из книги Х. Барендрегта, сс. 559 — 560.