
|
5.2.2. Теория
©
|

|
Докажем, что что число попарно неравных квадратов, из которых можно сложить какой-либо прямоугольник,
должно быть не меньше пяти.
Разумеется, ясно, что из двух неравных квадратов составить прямоугольник нельзя.
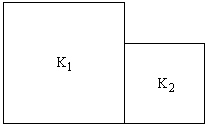
Более того, понятно (см. Рис. a), что нельзя составить прямоугольник и из трех
попарно неравных квадратов.
|
Рис. a.
Действительно, ведь два приложенных друг к другу квадрата образуют, по крайней мере,
один "пустой" угол, причем одна сторона этого "пустого" угла совпадает со стороной
меньшего из двух квадратов, так что его никак нельзя заполнить квадратом, отличным по величине
от уже имеющихся квадратов.
|
Аналогично можно доказать, что прямоугольник нельзя составить и из
четырех квадратов; однако нам будет удобнее
воспользоваться другим, несколько более общим соображением. А именно, докажем, что
если из какого-то числа попарно различных квадратов сложен прямоугольник
P, то квадраты, примыкающие к
самому маленькому квадрату K1,
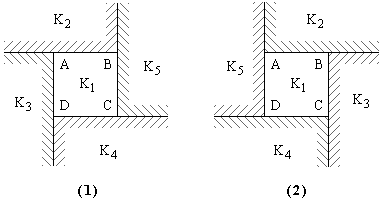
могут быть расположены только так, как это показано на следующем рисунке.
|
Рис. b.
То есть мы желаем доказать, что квадраты, примыкающие к
самому маленькому квадрату K1,
расположены либо так, как это изображено здесь слева, либо так, как это изображено справа
(эти два расположения несущественно отличаются друг от друга:
одно получается из другого симметрией относительно прямой).
|
Действительно, пусть K1 = ABCD —
самый маленький квадрат из числа тех, которые составляют прямоугольник P.
Очевидно, что, по крайней мере, к одной из сторон квадрата K1,
например к AB, примыкает сторона какого-то другого квадрата
K2. По предположению, сторона квадрата K2
больше AB; поэтому одна из вершин
A или B лежит внутри
стороны квадрата K2.
Пусть, например, этим свойством обладает вершина A.
Покажем, что в этом случае имеет место расположение, изображенное на Рис. b(1)
(если бы внутри стороны квадрата K2 лежала не вершина
A, а вершина B, то вместо расположения на
Рис. b(1) мы пришли бы к расположению Рис. b(2) ). Ясно, что возникающий при точке
A пустой угол должен быть заполнен некоторым квадратом
K3. По предположению, сторона квадрата K3
больше стороны AD; поэтому при вершине
D также образуется пустой угол, который должен заполняться квадратом
K4.
Аналогично, пустой угол при вершине C заполняется квадратом K5.
Так как сторона квадрата K5 больше CB,
то она выступает за точку B; поэтому правая вершина
квадрата K2 лежит на стороне AB
квадрата K1, т. е. или лежит внутри AB,
или совпадает с B.
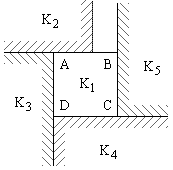
|
Рис. c.
Покажем, что в действительности имеет место второй случай. В самом деле,
если правая вершина квадрата K2 лежит внутри
стороны AB, то правая сторона квадрата и выступающая за
BC часть левой стороны квадрата K5
образуют "колодец", который уже квадрата K1 и поэтому может
быть заполнен лишь квадратами, меньшими, чем квадрат K1.
Но согласно сделанному нами предположению, таких квадратов нет.
|
Из доказанного утверждения сразу вытекают два следствия:
|
|

Число квадратов, из которых можно сложить прямоугольник P,
должно быть не меньше пяти.

Самый маленький квадрат должен лежать внутри прямоугольника P.
|


