|
|
9.3.1.1. Начало размышлений
о соотношении точек в континууме
©
|

|
Когда Кантор был ещё ребёнком, семья переехала из России в Германию, и именно там началось его обучение математике.
Защитив в 1868 г. диссертацию по теории чисел, он получил степень доктора в Берлинском университете.
Два года спустя он занял должность приват-доцента в Университете в Галле —
респектабельном учреждении, но не столь престижном для математиков, как университеты в Гёттингене или Берлине.
Один из его коллег в Галле, Генрих Эдуард Гейне, работал в то время над теорией тригонометрических рядов
и он побудил Кантора заняться сложной проблемой единственности таких рядов.
В 1872 г. в возрасте 27 лет Кантор опубликовал статью, содержавшую весьма общее решение этой проблемы,
в которой он использовал идеи, выросшие впоследствии в теорию бесконечных множеств.
Проблема, подсказанная Гейне, проистекает из трудов французского математика Жана Батиста Жозефа Фурье.
В 1822 г. Фурье показал, что график любой «достаточно гладкой» кривой (т.е. кривой, имеющей максимум конечное число точек разрыва)
может быть представлен всюду на интервале в виде суммы некоторого бесконечного тригонометрического ряда.
Другими словами, накладывая друг на друга бесконечное число синусоидальных и косинусоидальных колебаний,
каждую точку на этой «достаточно гладкой» кривой, за исключением точек разрыва, можно аппроксимировать с любой требуемой степенью
точности [см. рисунок ниже]. Говорят, что такой ряд сходится к кривой или функции,
за исключением конечного числа точек, или же сходится «почти всюду».
Результат Фурье имел большое значение, поскольку он указывал, что некоторые сложные функции могут быть представлены в виде суммы
синусов или косинусов, с которыми легче оперировать математически. Однако, чтобы оправдать такую замену, требовалось доказать,
что к функции сходится только один такой тригонометрический ряд.
Условия, при которых сходящийся к функции тригонометрический ряд является единственным, и начал исследовать Кантор.
В 1870 г. Кантор доказал, что если функция непрерывна всюду на интервале, то её представление тригонометрическим рядом единственно.
Его следующий шаг состоял в ослаблении требования непрерывности функции всюду на интервале.
Предположим, например, что график аппроксимируемой функции представляет собой прямую, параллельную оси
x, за исключением точки
x = 1/2, в которой функция принимает значение 0 вместо 1.
Кантор показал, что если условие сходимости в точке x = 1/2 и нарушается,
то всё равно существует единственный тригонометрический ряд, который сходится к этой функции в остальных точках.
То есть другого тригонометрического ряда, который мог бы аппроксимировать эту функцию, не существует.
Далее Кантор легко распространил свой результат на функции, имеющие любое конечное число точек разрыва,
которые он назвал исключительными точками.
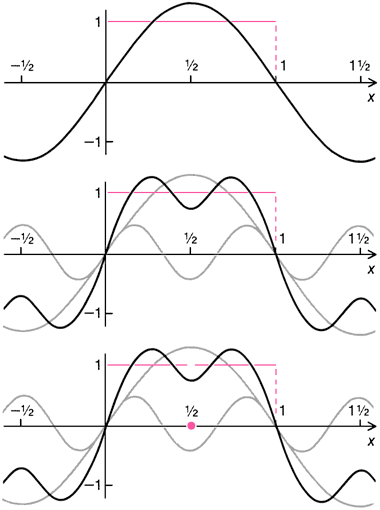
|
Гладкий непрерывный график, ординаты точек которого зависят от значений соответствующих точек на оси
x, можно с любой требуемой точностью аппроксимировать тригонометрическим рядом,
т.е. суммой синусов и косинусов.
Например, прямая горизонтальная линия, отстоящая на единицу длины вверх от оси
x (цветная), может быть аппроксимирована наложением синусоидальных колебаний
(серые кривые); изображены две первые стадии аппроксимации (чёрные кривые наверху и в середине).
Тригонометрический, аппроксимирующий график является единственным.
Однако, даже если график не непрерывен, его часто можно аппроксимировать единственным тригонометрическим рядом.
Например, если ординаты точек графика равны всюду единице, за исключением точки x = 1/2,
то тригонометрический ряд, сходящийся к непрерывной линии, сходится и к ломаной линии, за исключением точки
x = 1/2, (внизу).
Кантор показал, что график можно аппроксимировать единственным тригонометрическим рядом,
даже если число точек, в которых график не непрерывен, бесконечно, при условии,
что точки разрыва распределены на оси x некоторым специальным образом.
|
В 1872 г. Кантор публикует работу, представляющую собой важнейшее открытие.
Стремясь к более общей формулировке теоремы единственности, он доказал, что если исключительные
точки распределены на оси x некоторым специальным образом, то их может быть и бесконечно много.
Установить это можно было только на основе
точного описания бесконечного множества исключительных точек.
Однако для этого, как понимал Кантор, необходим
более глубокий анализ континуума точек на оси x. Так, исследуя сходимость тригонометрических рядов, Кантор постепенно начинает сосредоточивать своё внимание на соотношении точек в континууме.
Кантор принял за аксиому, что всякой точке непрерывной линии соответствует некоторое число, которое он назвал действительным числом,
чтобы отличить его от «мнимых» чисел, кратных
√ - 1.
Обратно, каждому действительному числу соответствует только одна точка прямой.
Следовательно, проблема описания континуума
точек прямой эквивалентна проблеме определения действительных чисел и исследованию их свойств.
Статья Кантора, опубликованная в 1872 г., имела большое значение ещё и потому, что в ней было дано изложение этих свойств.
Основную трудность в теории действительных чисел представляют такие числа, как
π
и
√ 2,
не являющиеся рациональными. (Рациональное число — это такое число, которое можно выразить в виде частного двух целых чисел.
Ещё в античности было известно, что
√ 2,
√ 3,
√ 5
и многие другие корни являются иррациональными.)
Так как правомерность рациональных чисел не вызывала сомнений, Кантор пошёл по пути, указанному Карлом Вейерштрассом, одним из его бывших учителей в Берлинском университете. Кантор предположил, что всякое иррациональное число может быть представлено
бесконечной последовательностью рациональных чисел.
Например, число
√ 2
можно представить бесконечной последовательностью рациональных чисел
1; 1,4; 1,41; ... . В соответствии с этим все иррациональные числа можно понимать как
геометрические точки числовой прямой, т.е. так же как и рациональные числа.
Несмотря на преимущества канторовского подхода, некоторые математики приняли его как вызов, поскольку он предполагал существование множеств или последовательностей чисел, имеющих бесконечно много элементов.
Философы и математики отвергали концепцию
завершённых бесконечностей со времён
Аристотеля главным образом вследствие тех
логических парадоксов, к которым, как казалось, они приводят. Например, Галилей указывал, что если в математике принять бесконечные завершённые множества, то чётных чисел должно быть столько же, сколько чётных и нечётных вместе. Всякому чётному числу можно сопоставить целое число, равное половине его величины, таким образом налицо
взаимно однозначное соответствие между элементами того и другого множества.
Некоторые теологи, например Фома Аквинский, также были против идеи завершённой бесконечности, считая её прямым вызовом единой и абсолютно бесконечной природе бога.
Чтобы избежать подобные возражения, математики стремились проводить чёткое различие между бесконечностью, рассматриваемой как завершённая величина, и бесконечностью, рассматриваемой как потенциальная, т.е. представляемой неопределённой суммой или рядом членов, стремящихся к некоторому пределу. Правомерной они считали лишь потенциальную бесконечность.
В 1831 г. своё отношение к завершённым бесконечностям Карл Фридрих Гаусс выразил словами, которые Кантор однажды назвал слишком категорическими. В письме Генриху Шумахеру Гаусс писал: «Что касается Вашего доказательства, я прежде всего протестую против применения бесконечной величины как завершённой, в математике это никак не допустимо. Понятие бесконечности есть лишь способ выражения понятия предела».
Говоря о пределах, можно было избежать парадоксов, связанных с актуальными бесконечностями. Например, прибавляя дополнительные цифры к десятичному разложению числа π, можно аппроксимировать истинное значение π с возрастающей точностью.
Однако Гаусс утверждал, что все члены десятичного разложения числа π не могут быть даны. Действительно, для точного определения π требовалось бы взять бесконечное число членов как что-то целое, другими словами, взять актуально бесконечное множество чисел — операция, которую Гаусс отказывался допускать.
Кантор не был одинок в изучении свойств континуума. В 1872 г., когда появилась его вышеуказанная статья, немецкий математик Рихард Дедекинд тоже опубликовал анализ континуума, основанный на бесконечных множествах.
В своей работе Дедекинд явно высказал идею, позднее уточнённую Кантором: «Прямая бесконечно более богата индивидуумами-точками, чем область... рациональных чисел индивидуумами-числами».
Сказанное можно представить следующим образом. Если на отрезке прямой рассмотреть распределение точек, соответствующих рациональным числам, то сколь бы малым ни был этот отрезок, на нём имеется бесконечно много рациональных точек.
Суть идеи Дедекинда состояла в том, что, несмотря на плотность рациональных точек на отрезке прямой, на нём всё же найдётся место, чтобы вставить бесконечное число иррациональных точек. Такая иррациональная точка, как π, попадает между рациональными точками, и таким образом множество рациональных чисел, хотя оно и всюду плотно, всё же разрежено, имеет «щели» и не является непрерывным.
Утверждение Дедекинда верно отражало суть понятия континуума, за исключением одного важного аспекта. Взяв идеи Дедекинда за основу, нельзя установить, насколько бесконечное множество точек континуума превышает бесконечное множество рациональных точек.
Великий вклад в решение этого вопроса был сделан Кантором, когда он в 1874 г. опубликовал свою статью «Об одном свойстве совокупности всех действительных алгебраических чисел» в «Журнале чистой и прикладной математики» Августа Леопольда Крелле, называемом также журналом Крелле, — наиболее авторитетном среди математиков периодическом издании того времени.
