
|
9.3.1.2. Идея взаимно-однозначного соответствия
©
|

|
Фактически Кантор воспользовался
указанным Галилеем парадоксом и превратил его в средство количественного сравнения бесконечных множеств. Он назвал два множества
эквивалентными, если между элементами этих множеств можно установить
взаимно однозначное соответствие.
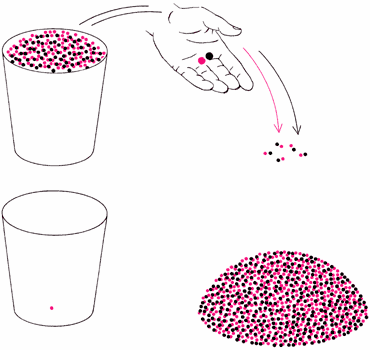
Предположим, у нас имеется ведёрко, заполненное чёрными и цветными шариками. Каким образом можно сравнить количество чёрных и цветных шариков?
Простейший способ состоит в извлечении шариков из ведёрка парами, состоящими из чёрного и цветного шариков. Если каждый шарик может быть объединён в пару с шариком другого цвета, то два множества эквивалентны. Если нет, то оставшиеся в ведёрке шарики показывают, каких шариков было больше.
|
Два множества можно сравнивать по величине, сопоставляя элементы одного множества с элементами другого.
Например, чтобы определить, каких шариков в ведёрке больше: цветных или чёрных, можно брать их из ведёрка парами, состоящими из цветного и чёрного шариков, до тех пор, пока там не останутся шарики одного цвета.
Именно этот остаток и указывает, каких шариков было больше. Такой же принцип Кантор применил для количественного сравнения бесконечных множеств.
|
Используя принцип взаимно однозначного соответствия, Кантор показал, что свойство, которое Галилей рассматривал как парадоксальное, фактически является естественным свойством бесконечных множеств.
Множество чётных чисел эквивалентно множеству всех целых положительных чисел, чётных и нечётных, вместе взятых, поскольку объединение в пары элементов каждого из этих множеств может быть осуществлено без опущения каких-либо элементов рассматриваемых множеств.

|
Целые числа можно одно за другим объединить в пары с чётными числами, не исчерпав какого-либо из множеств этих чисел.
То есть эти два множества имеют одинаковое число элементов.
Многие другие бесконечные множества тоже можно одно за другим сопоставить с целыми числами, т.е. фактически пересчитать.
Такие множества называются счётными.
|
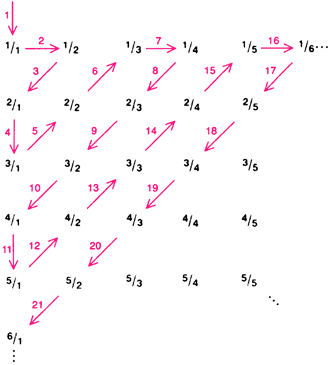
Кантор также предложил оригинальный способ объединения элементов множества всех рациональных чисел в пары с целыми числами [см. нижний рисунок].
|
Бесконечное множество рациональных чисел (т.е. чисел, которые можно представить как частное двух целых чисел) могло бы показаться значительно бoльшим, чем множество целых чисел. Например, между двумя любыми соседними целыми числами, допустим 0 и 1, имеется бесконечно много рациональных чисел.
Тем не менее в 1874 г. Кантор показал, что рациональные числа можно одно за другим объединить в пары с целыми числами.
Всякое рациональное число можно разместить в квадратной таблице, как показано на рисунке. Тогда каждое из них может быть связано с целым числом путём проведения цветной линии.
Таким образом, множество рациональных чисел является счётным.
|
Всякое множество чисел, элементы которого можно расположить один за другим или фактически сосчитать, используя множество целых положительных чисел, Кантор назвал счётным множеством.
При данной плотности рациональных чисел на прямой и относительной «разреженности» целых чисел, может показаться крайне противоречащим интуиции то, что эти два множества оказываются количественно эквивалентными.
Однако Кантор пошёл ещё дальше. Он доказал, что взаимно однозначного соответствия между множеством целых чисел и множеством всех точек на прямой, т.е. множеством действительных чисел, быть не может; одним словом, действительные числа образуют несчётное множество.
Кантор дал довольно сложное доказательство этого утверждения в своей статье, опубликованной в 1874 г. Я не буду останавливаться на нём, а изложу основную идею гораздо более простого, но более мощного способа доказательства, предложенного им в 1891 г.
Кантор начал своё доказательство с предположения, что существует взаимно однозначное соответствие между множеством действительных чисел и множеством целых чисел.
Последующим рассуждением показывается, что это предположение приводит к противоречию, отсюда следует, что первоначальное предположение неверно и такое взаимно однозначное соответствие невозможно.
Рассуждение можно упростить, рассматривая только множество действительных чисел, заключённых между 0 и 1. Если это множество больше множества целых чисел, то множество всех действительных чисел и подавно больше него.
Итак, предположим, что действительные числа, заключенные между 0 и 1, могут быть одно за другим объединены в пары с целыми числами. Установление такого соответствия эквивалентно составлению некоторого перечня действительных чисел, каждое из которых представляется как бесконечная десятичная дробь.
Но оказывается, что можно определить новое действительное число, не включённое в этот перечень.
Для того, чтобы показать это, берём первую цифру первого десятичного разложения в указанном перечне действительных чисел. Если эта цифра равна 1, то пишем 9 на первом месте после запятой. Если первая цифра в этом перечне не равна 1, то на первом месте определяемого числа пишем 1.
Построение нашего нового числа продолжается затем путём изменения второй цифры второго десятичного разложения в перечне, третьей цифры в третьем десятичном разложении и так далее.
Вновь построенное число должно отличаться по крайней мере одним десятичным знаком от каждого действительного числа, содержащегося в перечне, однако оно тем не менее представляет собой некоторое действительное число, расположенное между 0 и 1.
Поэтому можно построить некоторое число, не содержащееся в перечне действительных чисел, и таким образом предположение, что все действительные числа можно пересчитать, приводит к противоречию.
|
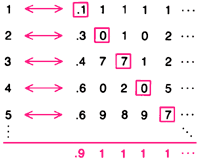
Множество действительных чисел, представленное континуумом точек на прямой, не является счётным. Если бы оно было счётным, то действительные числа, скажем между 0 и 1, можно было бы одно за другим объединить в пары с целыми числами.
Всякое действительное число в перечне можно представить бесконечным десятичным разложением (такие бесконечные десятичные дроби, как 0,5000..., представим в виде эквивалентной бесконечной дроби 0,4999...).
Каков бы ни был перечень таких десятичных дробей, можно построить новую десятичную дробь, которая определяет некоторое действительное число и не содержится в этом перечне.
Для этого на первом месте после запятой пишем 9, если первая цифра десятичного разложения первого действительного числа в перечне равна 1; в противном случае пишем 1. Аналогично изменяем вторую десятичную цифру во втором действительном числе, третью десятичную цифру в третьем и т.д.
Построенное десятичное разложение представляет некоторое действительное число, расположенное между 0 и 1, но оно должно отличаться по крайней мере одним десятичным знаком от каждого действительного числа, входящего в перечень.
Следовательно, предположение, что действительные числа можно объединить в пары с целыми числами, приводит к противоречию, а потому должно быть отброшено. Это доказательство основано на методе, называемом диагональным.
|

|
Вероятность случайного выбора точки, представляющей рациональное число, из континуума действительных чисел показывает, как множество рациональных чисел сравнивается по величине с множеством действительных чисел. Вероятность есть отношение числа рациональных точек к общему числу точек на некотором интервале.
Здесь интервал между 0 и 1 представлен окружностью свободно вращающегося колеса (на этом колесе 0 и 1 отождествляются). Предполагается, что вероятность остановки колеса в любой точке одинакова.
Точки, представляющие рациональные числа, бесконечно плотны в том смысле, что вдоль любой сколь угодно короткой дуги между двумя рациональными точками на окружности должно находиться бесконечное число рациональных точек. Несколько таких точек помечено.
Тем не менее множество всех точек на окружности бесконечно больше множества рациональных точек: вероятность, что колесо остановится в рациональной точке, равна нулю. Точнее эта вероятность меньше любой сколь угодно малой величины.
|
В августе 1874 г. Кантор женился на Валли Гутман. Супруги провели конец лета в горах Гарца, где они встретились с Дедекиндом. Этот период оказался чрезвычайно плодотворным для Кантора.
Несколько раньше в одном из своих писем Дедекинду Кантор писал: «Можно ли сопоставить поверхность (например, квадратную площадку, включая её границы) с отрезком прямой (включающим свои концы) таким образом, чтобы каждой точке поверхности соответствовала одна точка на этом отрезке, и наоборот?» Кантор полагал, что ответ должен быть отрицательным, но это требовало доказательства.
Однако в 1877 г. Кантор сообщает Дедекинду о своём поразительном результате: вопреки мнению, распространённому среди математиков, ему удалось доказать, что взаимно однозначное соответствие между точками прямой и точками плоскости возможно.
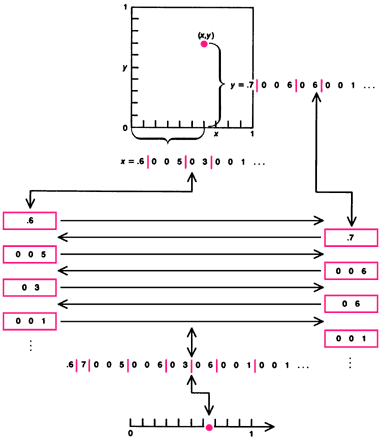
Доказательство состояло в представлении каждой точки квадрата парой десятичных дробей. Эти десятичные представления «перемешиваются» строго определенным образом, чтобы получить одно десятичное разложение, и эта десятичная дробь сопоставляется с точкой на отрезке прямой.
Весь этот процесс обратим [см. рисунок ниже]. Слова Кантора: «Я вижу это, но никак не могу этому поверить!» — говорят о том, насколько этот результат оказался неожиданным для него самого.
Кантор сразу же подготовил рукопись с описанием своего нового открытия, и послал её в
журнал Крелле. Работа эта послужила первым поводом для открытых столкновений между её автором и Кронекером.
Будучи редактором журнала, Кронекер имел право отказать в публикации любой статьи, работа же Кантора настолько шокировала его, что он не преминул этим правом воспользоваться.
Несмотря на то что Кантор представил свою рукопись 12 июля, для подготовки её к публикации ничего не делалось, и она не появилась в журнале в 1877 г.
Подозревая вмешательство Кронекера, Кантор пишет Дедекинду письмо, сетуя на неблагоприятное отношение к его рукописи. В письме он говорит также о своём желании забрать её из редакции. Однако Дедекинд, рассказав Кантору о собственном опыте в подобных делах, убедил его подождать, и оказался прав — статья наконец появилась в томе за 1878 г. Однако Кантор был настолько огорчён этим инцидентом, что отказался впредь публиковаться в журнале Крелле.
|
Между точками плоскости и точками прямой можно установить взаимно однозначное соответствие.
Каждая точка плоскости представляется парой бесконечных десятичных дробей и эти бесконечные дроби разбиваются на группы. Каждая цифра десятичного разложения, кроме нуля, начинает новую группу.
Затем эти группы комбинируются и превращаются в одну бесконечную десятичную дробь, представляющую точку на плоскости. Вся процедура обратима.
Аналогичное рассуждение показывает, что число точек любого конечномерного пространства эквивалентно числу точек на линии.
|





