Начало см. здесь здесь.

Отмеченная выше прямоугольная диаграмма Венна:

находится в интригующей близости также и к лексикографическому упорядочению на множестве всех двоичных наборов длины 3. Чтобы быть ближе к общепринятым определениям, повернем нашу прямоугольную диаграмму Венна, как показано ниже, и заменим вектор-столбцы вектор-строками:

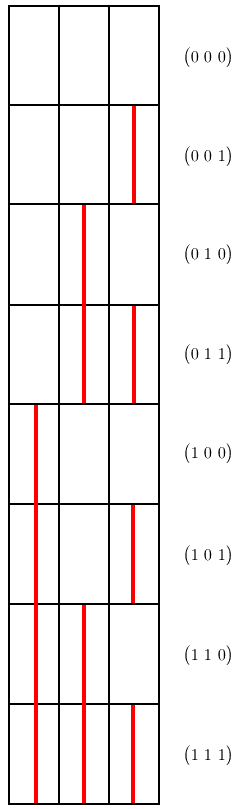
Выписанные справа рядом с каждым прямоугольником-строкой повернутой диаграммы соответствующие булевы вектор-строки образуют в совокупности хорошо известное в Computer Science лексикографическое упорядочение двоичных наборов длины 3:

Его можно посмотреть, например, здесь (для случая двоичных наборов длины 4).

Рассмотрение лексикографического упорядочения двоичных наборов в связи с триграммами кажется еще более оправданным, чем рассмотрение в их контексте соотношений для кода Хэммина. Оно представляется также более простым для постижения детьми, которые занимаются в детских IT-академиях.

2. Лексикографическое упорядочение двоичных наборов
в работе Лейбница

Лексикографическое упорядочение двоичных наборов длины 6 мы видим в пионерской работе Лейбница от 1703 года:

http://www.leibniz-translations.com/binary.htm

http://www.leibniz-translations.com/binary.htm

Лейбницу Лейбницево, но предлагаемый мною подход круче. Тестирование наличия имеющейся в нем линейной упорядоченности мы обеспечим методами логического программирования. В данном случае эти методы оказываются очень простыми и поэтому могут быть рекомендованы для первоначального изучения парадигмы логического программирования. Сказанное не означает, конечно, что об инсайте Лейбница нужно забыть. На самом деле инсайт Лейбница и мой собственный инсайт должны и будут гармонично сосуществовать вместе.

Джон Барвайс пишет:

Ну, а мы попробуем сделать следующий важный шаг по напралению к этой мечте.

3. Два способа "арифметической"
интерпретации двоичных наборов

Собственно говоря, у самого Фуси приведено только лишь само по себе лексикографическое упорядочение двоичных наборов; оно не требует для своей реализации каких-либо арифметических операций, а требует только лишь наличия некоторого линейного порядка на элементах бинарного алфавита (и у нас есть свобода в выборе самих этих элементов бинарного алфавита: это могут быть и традиционные 0 и 1, так и вообще любые два символа, например, V и H, как у меня).

Таким образом, для собственно уже "арифметической" интерпретации двоичных наборов, имеются различные варианты. На примере небольшого фрагмента Лейбницевской таблицы, приведенной выше, можно показать различие между этими вариантами. На рисунке ниже слева указан вариант, предлагаемый Лейбницем, а справа указан вариант, предлагаемый мной:

Связь между дробями и цепочками в алфавите {V, H} объясняется здесь. Приведенный пример соответствует лексикографическому упорядочению цепочек длины 6 в алфавите {V, H}, с которыми ассоциированы дроби, расположенные на 6-ом уровне Дерева Штерна - Броко (это соответствие очень подробно объясняется здесь на примере 2-го уровня Дерева Штерна - Броко).

У Лейбница мы имеем: 16 < 17 < 18. В моем случае, как нетрудно проверить, выполняется: 6 / 11 < 9 / 16 < 11 / 9.

4. Лексикографическая сортировка

Нам понадобятся также знания о методах лексикографической сортировки цепочек в бинарном алфавите, относительно которых можно справиться, например, в монографии Ахо - Хопкрофта - Ульмана здесь и здесь.