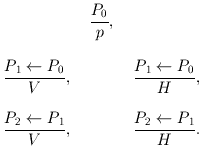|
12.6.1.2. Начало построения акционального универсума, отвечающего базовому фрагменту УСК
|

|
1. Начала информатики предшествуют началам арифметики
Такой вывод можно сделать исходя из
современных интерпретаций "Книги Перемен".
Это подтверждается и тем, что говоря о смысле основополагающих конструкций
"Книги Перемен" (или "И Цзин"),
обычно используют терминологию информатики, например, используют термин
"файлы":
Эти символы на современном языке можно считать самым примитивным банком данных для хранения информации. Именно концепция инь и ян позволила открыть двоичную систему счисления, лежащую в основе современной вычислительной техники. Но все равно, возможности 8 триграмм ограничены и мы нуждаемся в более объемных файлах для сохранения огромных объемов информации.
В своем
Курсе Математики я планирую значительно усилить этот тренд.
Именно для того, чтобы еще больше усилить тенденцию, укреплению которой спобствовал и выход
книги Д. Кнута и др.:
превращать малограмотных школьников в прекрасных математиков.
2. Роль УСК В.В. Мартынова в этом деле
На протяжении более 15 лет, начиная с 1983 года, я работал в группе
“Семантика” под руководством В. В. Мартынова, занимавшейся
исследованиями в области Искусственного Интеллекта.
В дискуссиях с основателем УСК, у меня постепенно сформировалась та концепция, которую я положил в основу продвигаемой сейчас идеи. В конце своей жизни В. В. Мартынов согласился с моим предложением об использовании
комбинатора B
для интерпретации базового фрагмента УСК.
В конце концов выяснилось, что
базовый фрагмент УСК степени 3
естественным образом описывает “модель мира” , которая
довольно-таки четко изложена в китайской “Книге перемен”:
В линейной упорядоченности триграмм по Фуси реализован принцип "Си цы чжуани": "Цянь (Небо) и Кунь (Земля) формируют ряд, и перемены устанавливаются внутри него".
Я решил положить этот факт в фундамент некоторого систематического курса математики, в котором из этого “первоначала” естественным образом выводилась бы вся школьная математика вместе с Computer Science.
В самое ближайшее время я очень подробно опишу, каким образом эта
"китайская модель мира"
может быть представлена в виде соответствующего
акционального универсума.
А пока представляю начало построения акционального универсума для простейшего случая, отвечающего семантике так называемой "реальной цепочки" из базового фрагмента УСК порядка 2.
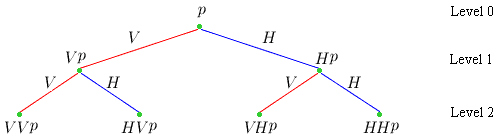
3. Простейший случай n = 2
Категорное имя
P2 обозначает
базисную категорию,
состоящую из
четырех цепочек
VVp, HVp, VHp, HHp,
расположенных на втором уровне Дерева
(интуитивный смысл функциональных символов
V и
H, с помощью которых формируются
термы
VVp, HVp, VHp, HHp, можно посмотреть
здесь).
Для сборки цепочек из указанных категорий предлагается
исчисление локализованных цепочек
(LCC) со следующим набором из пяти аксиом:
Например, цепочка
HVp,
принадлежащая категории
P2,
может быть собрана
в данном
LCC следующим образом
(правила сборки в
LCC в общем случае изложены
здесь):
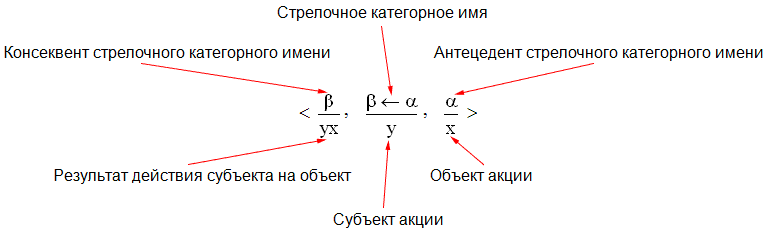
Каждое правило вывода является акцией:
состоящей из шести компонентов:
Базовые интуиции для такого подхода
к экспликации понятия "акция" приведены
здесь.
Уточнение этих интуиций для
Исчисления Локализованных Цепочек (
LCC) изложено
здесь
(в этом случае результатом действия субъекта
y на объект
x является
конкатенация
yx
цепочек
y и
x).