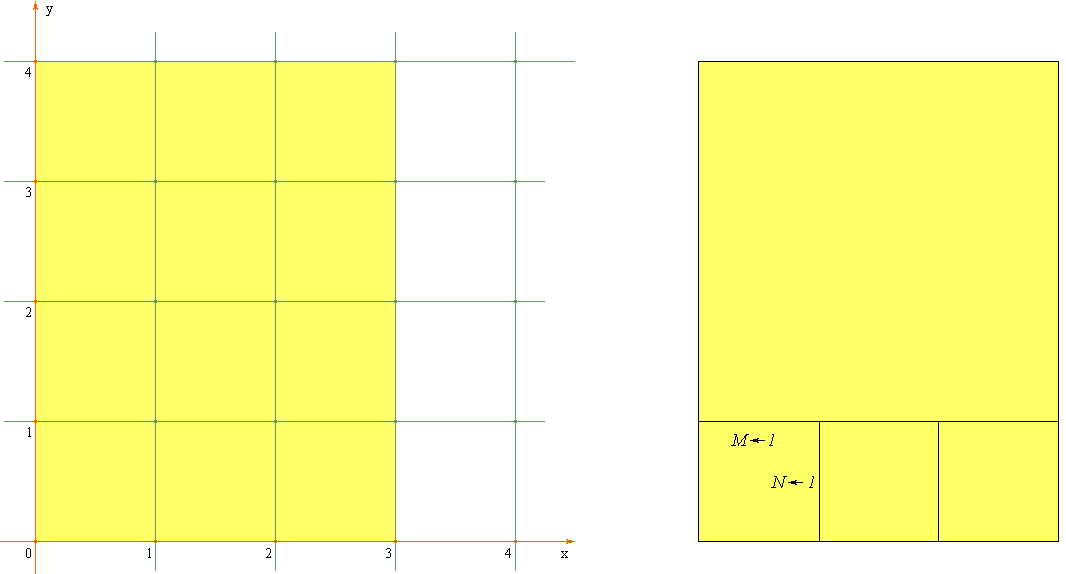Начало см. здесь и здесь.

При доказательствах несоизмеримости можно использовать факт "зацикливания" антанаиресиса в этой ситуации (очень подробное разъяснение этого феномена см. у Б. Л. ван дер Вардена здесь; правда, не для корня из двух, а для корня из трех).

Доказательство, предложенное Б. Л. ван дер Варденом, требует использования определенных методов геометрической алгебры, в частности, определенных манипуляций с гномоном. Я рассмотрел некоторые из этих манипуляций (уже именно для случая корня из двух) в контексте очень наглядного, на мой взгляд, построения "геометрических двойников" целых чисел вещественного квадратичного поля .

То, что здесь сейчас было сказано об антанаиресисе, не есть самое простое, что можно сказать об этом алгоритме. Но на самом деле антанаиресис очень прост. Именно поэтому его естественно было бы попробовать выбрать в качестве начала при обучении программированию.

2. Антанаиресис как начало при обучении программированию

Ниже изображена блок-схема антанаиресиса в стиле, предписываемом методологией структурного программирования.

Дональд Кнут считал, что обучение программированию может быть начато с алгоритма Евклида, с которым одно время ассоциировалось само это слово: "алгоритм". Но антанаиресис не совпадает с тем, что обычно формулируют как "алгоритм Евклида" (хотя, конечно, эти два алгоритма тесно связаны друг с другом). Для дальнейшего нам будет очень важно подчеркнуть это различие. По той причине, в частности, что именно антанаиресис очень естественным образом порождает Дерево Штерна-Броко.

Этот факт является одним из подтверждений ранее высказанного утверждения о том, что все четыре суперпаттерна: полного бинарного дерева, антанаиресиса, плотного линейного порядка и гармонической сопряженности теснейшим образом связаны друг с другом.

3. Полезная графическая метафора для антанаиресиса

Изображенная ниже известная графическая метафора для антанаиресиса теперь приведена в новом виде, согласованном с реалиями плоской квадратной целочисленной решетки точек. Так нам будет удобнее для дальнейшего изложения.

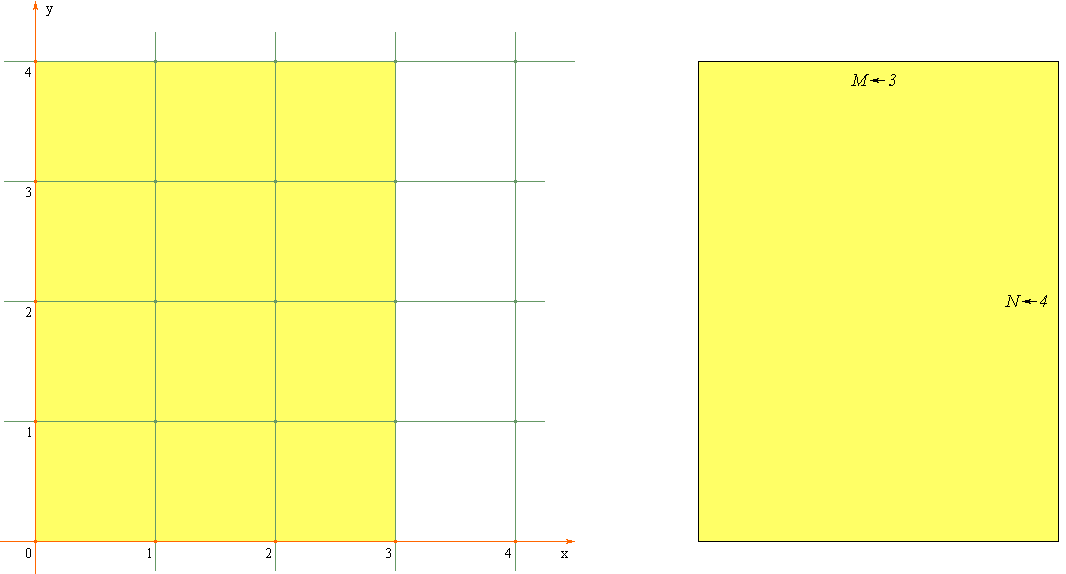
В этом новом виде на каждом шаге максимально возможный квадрат вписывается в "текущий прямоугольник" либо сверху, либо справа. При помощи этой графической метафоры мы можем очень наглядно испытать антанаиресис для какого-нибудь конкретного набора входных значений (например, для случая M = 3 и N = 4) по аналогии с тем, как Дональд Кнут делал это словесно для "алгоритма Евклида".

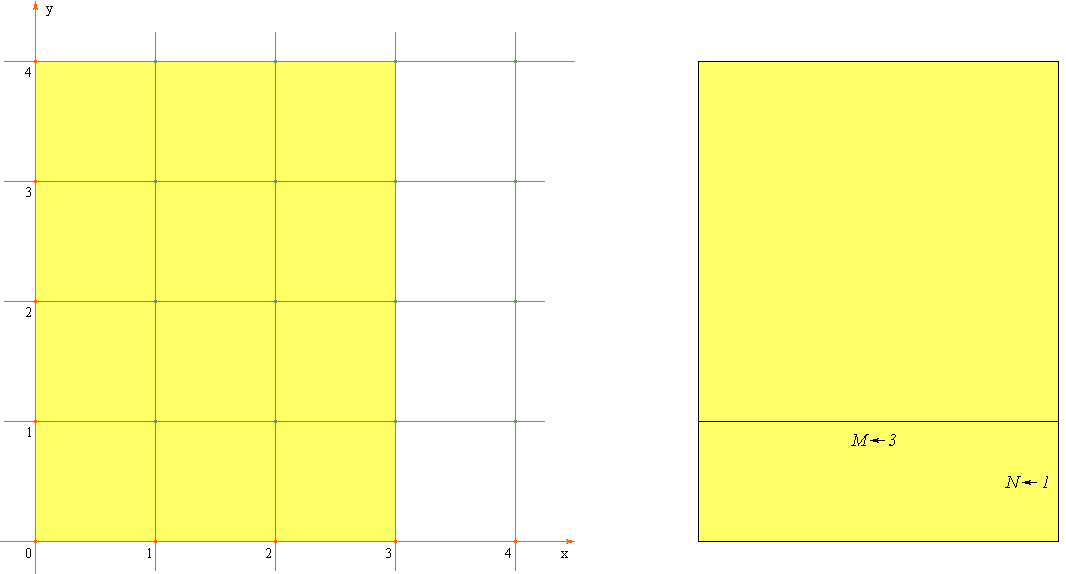
На данном этапе утверждение "M не равно N" является истинным, поэтому в соответствии с блок-схемой алгоритма мы переходим к анализу утверждения "M > N". В данном случае утверждение "M > N" является ложным, поэтому в соответствии с блок-схемой алгоритма мы выполняем действие , которое визуально моделируется вписыванием в текущий прямоугольник максимально возможного квадрата сверху:

После выполнения предыдущего действия значениями переменных M и N являются натуральные числа 3 и 1, соответственно. В соответствии с блок-схемой алгоритма переходим к анализу утверждения "M не равно N". В данном случае это утверждение является истинным. Поэтому в соответствии с блок-схемой алгоритма переходим к анализу утверждения "M > N". В данном случае утверждение "M > N" является истинным. Поэтому в соответствии с блок-схемой алгоритма выполняем действие , которое визуально моделируется вписыванием в текущий прямоугольник максимально возможного квадрата справа:

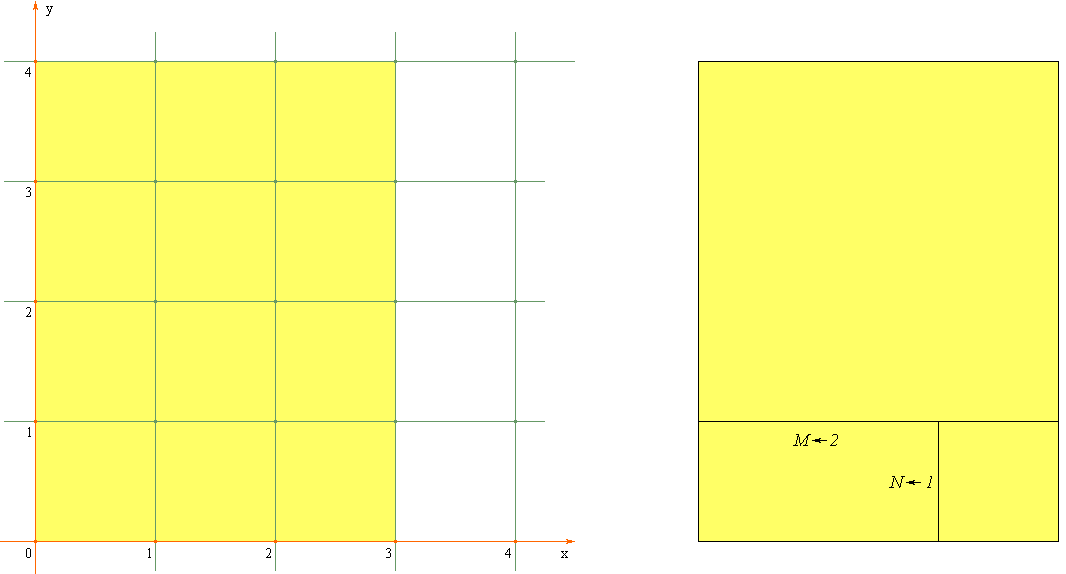
После выполнения предыдущего действия значениями переменных M и N являются натуральные числа 2 и 1, соответственно. В соответствии с блок-схемой алгоритма переходим к анализу утверждения "M не равно N". В данном случае это утверждение является истинным. Поэтому в соответствии с блок-схемой алгоритма переходим к анализу утверждения "M > N". В данном случае утверждение "M > N" является истинным. Поэтому в соответствии с блок-схемой алгоритма выполняем действие , которое визуально моделируется вписыванием в текущий прямоугольник максимально возможного квадрата справа:

После выполнения предыдущего действия значениями переменных M и N являются натуральные числа 1 и 1, соответственно. В соответствии с блок-схемой алгоритма переходим к анализу утверждения "M не равно N". В данном случае это утверждение является ложным. Поэтому в соответствии с блок-схемой алгоритма выполнение алгоритма заканчивается. Результирующими значениями переменных M и N являются натуральные числа 1 и 1, соответственно.